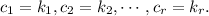Question

Given that v1, v2, · · · , vr are basis of a vector space V . Suppose for some vector u in V , we have u = c1v1 + c2v2 + · · · + crvr, and the same vector u can also be expressed as u = k1v1 + k2v2 + · · · + krvr. Show that ci must be equal to ki for all i = 1, 2, · · · r. Do not cite any theorem, do it from definition, nothing fancy.

Answer 1

We have that
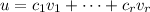`u=c_1v_1+\cdots+c_rv_r`v and
`u=k_1v_1+\cdots k_rv_r`

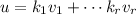
matching these two expression,

`c_1v_1+\cdots+c_rv_r=k_1v_1+\cdots k_rv_r\\(c_1-k_1)v_1+\cdots+(c_r-k_r)v_r=0`

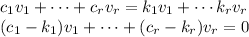
The last expression show the zero vector as linear combination of the vectors of the basis. But this vectors are linear independent, then the coefficients of the linear combination must be zero. That is,

`c_1-k_1=0, c_2-k_2=0, \cdots , c_r-k_r=0`

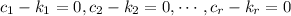
This implies that

`c_1=k_1, c_2=k_2,\cdots, c_r=k_r.`