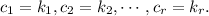Answer:
We have that
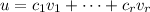 v and
v and
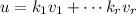
matching these two expression,
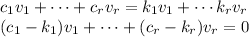
The last expression show the zero vector as linear combination of the vectors of the basis. But this vectors are linear independent, then the coefficients of the linear combination must be zero. That is,
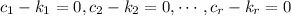
This implies that