Answer:
The choices were typed wrong, but we can find the inverse of each option.
For function
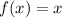 the inverse is the same function
the inverse is the same function
 , because an inverse of a function is where their composition gives the independent variable as unique result.
, because an inverse of a function is where their composition gives the independent variable as unique result.
If we do that with each function, we have:
 ; where
; where
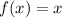 and
and
 , we have
, we have
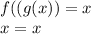
So they are inverse.
For
 its inverse would be
its inverse would be
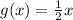 , because
, because
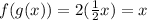
For
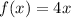 , its inverse is
, its inverse is
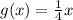 , because
, because
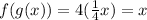
For
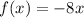 , its inverse is
, its inverse is
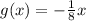 , because
, because
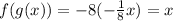
There you have all inverses. Basically, if their composition results in
 , that means they are inverse.
, that means they are inverse.