Answer:
The dimensions of the rectangular volleyball court are 60 ft x 30 ft
Explanation:
Let
x ----> the length of rectangular volleyball court
y ---> the width of the rectangular volleyball court
we know that
The area of the rectangular volleyball court is equal to
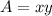
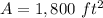
so
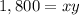 ----> equation A
----> equation A
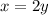 -----> equation B
-----> equation B
substitute equation B in equation A
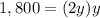
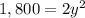
Solve for y
Simplify
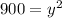
take square root both sides
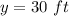
Find the value of x
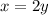
substitute the value of y
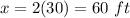
therefore
The dimensions of the rectangular volleyball court are 60 ft x 30 ft