Question

An image 60.0 mm long is formed on a wall located 2.30 m away from a source of

light 20.0 mm high. What is the magnification? What is the focal length of this
mirror? Is it diverging or converging?
(-3.00, 0.862 m)​

Answer 1

Missing info in the text: the image is inverted

1) Magnification: -3

The magnification can be calculated with the equation

`M=(y')/(y)`

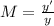
where

y' is the size of the image

y is the size of the object

In this problem, we have

y' = -60.0 mm (the sign is negative since the image is inverted)

y = 20.0 mm

Substituting,

`M=(-60)/(20)=-3`

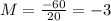
2) Focal length: 0.862 m (converging)

We can also rewrite the magnification as follows

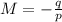`M=-(q)/(p)` (1)

where

q is the distance of the image from the mirror

p is the distance of the image from the mirror

Here we know that the distance between the image and the object is 2.30 m, so

`q-p=2.30`

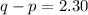
which means

`q=p+2.30`

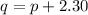
Substituting into (1), we can find p:

`M=-3=-(p+2.30)/(p)\\3p=p+2.30\\2p = 2.30\\p = 1.15 m`

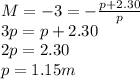
And also q:

`q=p+2.30=1.15+2.30 = 3.45 m`

So now we can finally find the focal length by using the lens equation:

`(1)/(f)=(1)/(p)+(1)/(q)`

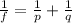
Where f is the focal length. Solving for f,

`f=(pq)/(p+q)=((1.15)(3.45))/(1.15+3.45)=0.862 m`

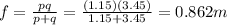
And since the focal length is positive, it means that the mirror is converging.