Question

Some sliding rocks approach the base of a hill with a speed of 12 m/s. The hill rises at 36° above the horizontal and has coefficients of kinetic friction and static friction of 0.45 and 0.65, respectively, with these rocks. (a) Find the acceleration of the rocks as they slide up the hill. (b) Once a rock reaches its highest point, will it stay there or slide down the hill

Answer 1

(a)
`9.33(m)/(s^2)`

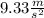
(b) The rocks slide down the hill.

Step-by-step explanation:

According to Newton's second law, we have these equations from the free body diagram of the rocks:

`\sum F_x:f_k+W_x=ma_x\\\sum F_y:N-W_y=0`

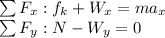
The components of weight are given by:

`W_x=mgsen(36^\circ)\\W_y=mgcos(36^\circ)`

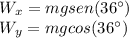
Recall that the kinetic frictional force is defined as:

`f_k=\mu_kN`

(a) Solving for
`a_x` and replacing:

`N=W_y\\N=mgcos(36^\circ)\\f_k=\mu_kmgcos(36^\circ)\\a_x=(f_k+W_x)/(m)\\a_x=(\mu_kmgcos(36^\circ)+mgsin(36^\circ))/(m)\\a_x=g[\mu_kcos(36^\circ)+sin(36^\circ)]\\a_x=9.8(m)/(s^2)[0.45cos(36^\circ)+sin(36^\circ)]\\a_x=9.33(m)/(s^2)`

(b) Since on the x-axis it is the axis on which there is motion and in this case the two forces are in opposite direction, we must calculate which force is greater to answer this question.

`\sum F_x:W_x-f_s=ma_x\\f_s=\mu_s mgcos(36^\circ)\\f_s=0.65mg(0.81)\\f_s=0.53mg\\W_x=mgsin(36^\circ)\\W_x=0.59mg`

The x-component of the weight is greater than the static frictional force, therefore the rocks slide down the hill.