Question

A man claims that he can hold onto a 15.0-kg child in a head-on collision as long as he has his seat belt on. Consider this man in a collision in which he is in one of two identical cars each traveling toward the other at 62.0 mi/h relative to the ground. The car in which he rides is brought to rest in 0.08 s. (a) Find the magnitude of the average force needed to hold onto the child.

Answer 1

F= 5195.625 N

Step-by-step explanation:

To obtain the force needed to hold the child, we need to know the aceleration in which the car is breaking.

Aceleration is equal to velocity divided by the time of breaking

In international system, velocity [m/s] is

v= (62 mi/h)*(1609 m/mi)*(1 h/3600 s)

v= 27.71 m/s

Now, we part the velocity by the time that is 0.08 seconds

a= v/t= (27.71 m/s)/(0.08 s)

a= 346.375 m/
`s^(2)`

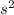
The force in agreement with the Newton's second law is

F=m*a = 15 Kg*346.375 m/
`s^(2)`

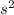
F= 5195.625 N

(Note: 1 N = 1 Kg*m/
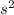`s^(2)`)