Question

Consider a value to be significantly low if its z score less than or equal to minus2 or consider a value to be significantly high if its z score is greater than or equal to 2. A test is used to assess readiness for college. In a recent​ year, the mean test score was 21.3 and the standard deviation was 5.1. Identify the test scores that are significantly low or significantly high. What test scores are significantly​ low? Select the correct answer below and fill in the answer​ box(es) to complete your choice. A. Test scores that are between nothing and nothing. ​(Round to one decimal place as needed. Use ascending​ order.) B. Test scores that are less than nothing. ​(Round to one decimal place as​ needed.) C. Test scores that are greater than nothing. ​(Round to one decimal place as​ needed.)

Answer 1

The significantly low scores are those that are less than 11.1.

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by

`Z = (X - \mu)/(\sigma)`

In this problem, we have that:

In a recent​ year, the mean test score was 21.3 and the standard deviation was 5.1. This means that
`\mu = 21.3, \sigma = 5.1`.

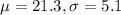Consider a value to be significantly low if its z score less than or equal to -2;

The significant low scores are between 0 and X when
`Z = -2`. So these scores are the ones that are less than X when
`Z = -2`.

`Z = (X - \mu)/(\sigma)`

`-2 = (X - 21.3)/(5.1)`

`X - 21.3 = -10.2`

`X = 11.1`

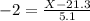
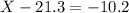
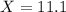
The significantly low scores are those that are less than 11.1.