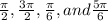Answer:
third option:
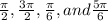
Explanation:
We write the sin(2x) using the property of sin of the double angle:
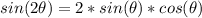 and replace the expression on the left of the given equation by this:
and replace the expression on the left of the given equation by this:
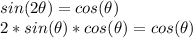
now we notice that if
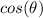 equals zero, the equation becomes true. Therefore all of the values
equals zero, the equation becomes true. Therefore all of the values
 that make
that make
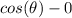 are solutions. That is
are solutions. That is
 .
.
Now, in the case
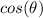 is NOT zero, we can divide both sides of the equation by it, ending up with a simple answer:
is NOT zero, we can divide both sides of the equation by it, ending up with a simple answer:
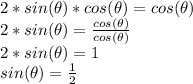
and in the interval between 0 and
 the solutions to this are:
the solutions to this are:
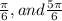
So we found a total of four solutions: