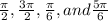Question

Solve sin 2ø= cos ø on the interval 0

Answer 1

third option:
`(\pi )/(2) , (3\pi )/(2) , (\pi )/(6) , and (5\pi )/(6)`

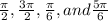
Explanation:

We write the sin(2x) using the property of sin of the double angle:

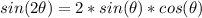`sin(2\theta)=2*sin(\theta)*cos(\theta)` and replace the expression on the left of the given equation by this:

`sin(2\theta)=cos(\theta)\\2*sin(\theta)*cos(\theta)=cos(\theta)`

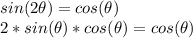
now we notice that if
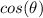`cos(\theta)` equals zero, the equation becomes true. Therefore all of the values
`\theta` that make
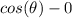`cos(\theta)-0` are solutions. That is
`\theta=(\pi )/(2) and \theta=(3\pi )/(2)`.

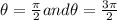Now, in the case
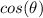`cos(\theta)` is NOT zero, we can divide both sides of the equation by it, ending up with a simple answer:

`2*sin(\theta)*cos(\theta)=cos(\theta)\\2*sin(\theta)=(cos(\theta))/(cos(\theta)) \\2*sin(\theta)=1\\sin(\theta)=(1)/(2)`

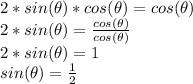
and in the interval between 0 and
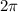`2\pi` the solutions to this are:

`(\pi )/(6) , and (5\pi )/(6)`

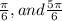
So we found a total of four solutions:
`(\pi )/(2) , (3\pi )/(2) , (\pi )/(6) , and (5\pi )/(6)`