Question

You are playing a dice game. The object of the game is to roll a certain combination of numbers in a single toss of two dice. Your dice are 'fair', but your opponent likes to win, and his dice are 'loaded' such that a four has a 7/36 probability of landing upwards. That means that the opposite side of four is counter-loaded (the opposite sides of a die adds to seven). What is the probability of your opponent rolling two even numbers? Give your answer as a decimal value, not a percent.

Answer 1

There is a 0.2785 probability of your opponent rolling two even numbers.

Explanation:

Since we are looking for the probability of rolling even numbers, we must consider the odds of rolling a 2, a 4 or a 6.

A fair dice would yield in a 6/36 chance of rolling each number, but since these dice are loaded, there is a 7/36 chance of rolling a 4 and a 5/36 chance of rolling a 3 (opposite side of 4); the probabilities for rest remain the same.

Therefore, the probability (P1) of rolling and even number in one die is:

`P_(1) = P(2) + P (4) + P (6)\\P_(1) = (6)/(36) + (7)/(36) +(6)/(36) \\P_(1) = (19)/(36)`

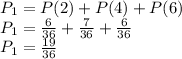
Since the game involves two dice, the probability of rolling even numbers on both is:

`P_(2) = P_(1) ^(2)\\P_(2) = ((19)/(36)) ^(2)\\P_(2) =0.2785`

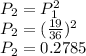
There is a 0.2785 probability of your opponent rolling two even numbers.