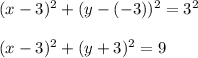Question

Find an equation of the circle:

Center on line x–y = 6, tangent to both axes



I NEED HELP QUICK 98 POINTSSSSS!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answer 1

`(x-3)^2+(y+3)^2=9`

Explanation:

If the center of the circle lies on the line y-x=6, then it has coordinates (x,6-x).

If this circle is tangent to both axes, then it is tangent

• to the x-axis at point (x,0);
• to the y-axis at point (0,6-x).

Find the radii as distances between the center and the tangent points:

`r=√((x-x)^2+(6-x-0)^2)=|6-x|\\ \\r=√((x-0)^2+(6-x-(6-x))^2)=|x|`

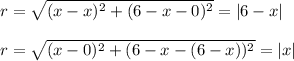
Equate them:

`|6-x|=|x|\\ \\(6-x)^2=x^2\\ \\x^2-12x+36=x^2\\ \\12x=36\\ \\x=3\\ \\x-6=3-6=-3`

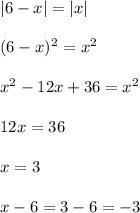
Thus, the center is at point (3,-3) and the radius is |3|=3.

The equation of the circle is

`(x-3)^2+(y-(-3))^2=3^2\\ \\(x-3)^2+(y+3)^2=9`