The mass of the copper cylinder is 177065.856g
Given:
Radius of the copper cylinder R=12cm
Height of the copper cylinder H=44cm
Density of the cylinder=8.90

To find:
Mass of the copper cylinder
Step by Step by explanation:
Solution:
According to the formula, Mass can be calculated as
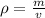 and from this
and from this
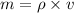
Where, m=mass of the cylinder
 =density of the cylinder
=density of the cylinder
v=volume of the cylinder
And also cylinder is provided with radius and height value.
So volume of the cylinder is calculated as
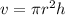
Where
 =3.14
=3.14
r=radius of the cylinder=12cm
h=height of the cylinder=44cm
Thus,
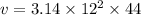
v=3.14 \times 144 \times 44
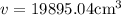
And we know that,
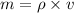
Substitute the known values in the above equation we get
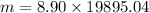
m=177065.856g or 177.065kg
Result:
Thus the mass of the copper cylinder is 177065.856g