Question

A 0.200 g sample of magnesium and zinc is placed in a rigid 1 L vessel containing dry air at 25 °C and 1 atm. The magnesium and zinc are treated with dilute sulfuric acid to produce hydrogen gas according to the following balanced reactions: Mg (s) + H2SO4 (aq) → Mg2+ (aq) + SO42– (aq) + H2 (g) Zn (s) + H2SO4 (aq) → Zn2+ (aq) + SO42– (aq) + H2 (g) The hydrogen gas is then completely combusted in the same vessel to form water as a product. The vessel is then cooled back to 25 °C (assume that all the water condenses) and the pressure is found to be 0.95 atm. What is the mass percentage of magnesium in the mixture?

Answer 1

Djdhhdhdhdhdhdhdhdhdhdhdhdvfvdfh

Answer 2

`67.3\% Mg`

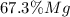
Step-by-step explanation:

Hello,

In this case, one first must consider the final pressure in order to compute the consumed hydrogen mass converted into water as shown below, considering the ideal gas equation for the gaseous water:

`n_(H_2O)=(P_2V)/(RT)=(0.16atm*1L)/(0.082(atm*L)/(mol*K)*298.15K)=0.00655mol`

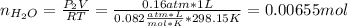
Next, taking into account the hydrogen combustion process:

`2H_2+O_2\rightarrow 2H_2O`

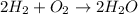
One computes the consumed hydrogen mass during as follows:

`m_(H_2)=0.00655molH_2O*(2molH_2)/(2molH_2O)*(2gH_2)/(1molH_2)=0.0131gH_2`

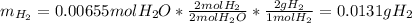
Now, such mass equals the yielded hydrogen during sample's treatment with dilute sulfuric acid:

`Zn+H_2SO_4\rightarrow H_2+ZnSO_4\\Mg+H_2SO_4\rightarrow H_2+MgSO_4`

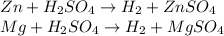
Thereby, by means of both reactions, the hydrogen mass equals:

`m_(H_2)=0.0131gH_2=m_(H_2)^(Mg)+m_(H_2)^(Zn)`

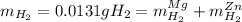
Whereas
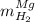`m_(H_2)^(Mg)` accounts for the hydrogen yielded by the magnesium and
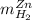`m_(H_2)^(Zn)` by the zinc which are computed in terms of the stoichiometry and the initial sample's composition as shown below:

`m_(H_2)^(Mg)=\% Mg*0.200g\ sample*(1molMg)/(24.305gMg)*(1molH_2)/(1molMg)*(2gH_2)/(1molH_2)`

`m_(H_2)^(Zn)=\% Zn*0.200g\ sample*(1molZn)/(65.409gZn)*(1molH_2)/(1molZn)*(2gH_2)/(1molH_2)`

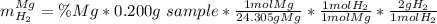
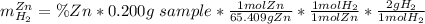
Now, as the addition between the percentages equals one, the mass of hydrogen due to zinc could be rewritten as:

`m_(H_2)^(Zn)=(1-\% Mg)*0.200g\ sample*(1molZn)/(65.409gZn)*(1molH_2)/(1molZn)*(2gH_2)/(1molH_2)`

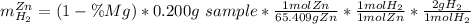
In such a way, one obtains:

`0.0131gH_2=0.0165\% Mg+0.00611gH_2-0.00611\% Mg\\\\\% Mg=(0.0131-0.00611)/(0.0165-0.00611)=0.673=67.3\% Mg`

Best regards.