Question

The U.S. Energy Information Administration (US EIA) reported that the average price for a gallon of regular gasoline is $3.94 (US EIA website, April 6, 2012). The US EIA updates its estimates of average gas prices on a weekly basis. Assume the standard deviation is $.25 for the price of a gallon of regular gasoline and recommend the appropriate sample size for the US EIA to use if they wish to report each of the following margins of error at 95% confidence. a. The desired margin of error is $.10. b. The desired margin of error is $.07. c. The desired margin of error is $.05.

Answer 1

a) 25

b) 49

c) 97

Explanation:

The sample size is calculated using the formula, n =
`(\frac{\sigma* z}{\textup{Margin of error}})^2`

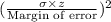
Now,

for 95% confidence level value of z-factor = 1.96

Given:

Mean = $3.94

standard deviation = $0.25

thus,

a) for margin of error = $0.10

n =
`(\frac{\sigma* z}{\textup{Margin of error}})^2`

or

n =
`(\frac{0.25*1.96}{\textup{0.10}})^2`

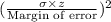
or

n = 4.9²

or

n = 24.01 ≈ 25 (Rounded off to next integer)

b) for margin of error = $0.07

n =
`(\frac{\sigma* z}{\textup{Margin of error}})^2`

or

n =
`(\frac{0.25*1.96}{\textup{0.07}})^2`

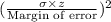
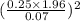
or

n = 7²

or

n = 49

c) for margin of error = $0.05

n =
`(\frac{\sigma* z}{\textup{Margin of error}})^2`

or

n =
`(\frac{0.25*1.96}{\textup{0.05}})^2`

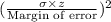
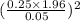
or

n = 9.8²

or

n = 96.04 ≈ 97 (Rounded off to next integer)