Answer:
A. P("Jury of 6 students")=0.000036
B. P("Jury of 6 members of the faculty")=0.06324
C. P("Jury of 2 students and 4 members of the faculty")=0.39528
Explanation:
A. First notice that we are dealing with an hypergeometric distribution of probability (We have that the total sample is divided in 2 different groups from where you want to select certain number of objects randomly), so we can use the formula of hypergeometric probability for 2 groups:
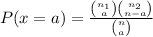
Where n₁ is the number of objects in group 1, n₂ the same but for group 2, n is the total of objects in two groups and a is the number of people we want in group 1 (depending what you consider success).
Now we are able to find the probability that we were asked for:
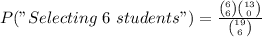
Notice I set a (being 6) under n₁ (group of students). That equation give us:
P("Jury of 6 students") = 0.000036
B. We use the same idea but we want to select people just from the faculty members:
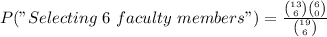
Notice i set a (being 6) under n₂ (group of the faculty), and I just changed the order. We get
P("Jury of 6 members of the faculty")=0.06324
C. Now we select people from the 2 groups, but its the same idea.
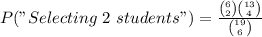
Notice "Selecting 2 students" automatically makes that you choose 4 faculty members, so you could´ve set it as "Selecting 4 faculty members" and it would be the same. When we solve, it results in
P("Jury of 2 students and 4 members of the faculty")=0.39528