Question

The grade appeal process at a university requires that a jury be structured by selecting six individuals randomly from a pool of six students and thirteen faculty.​ (a) What is the probability of selecting a jury of all​ students? (b) What is the probability of selecting a jury of all​ faculty? (c) What is the probability of selecting a jury of two students and four ​faculty?

Answer 1

A. P("Jury of 6 students")=0.000036

B. P("Jury of 6 members of the faculty")=0.06324

C. P("Jury of 2 students and 4 members of the faculty")=0.39528

Explanation:

A. First notice that we are dealing with an hypergeometric distribution of probability (We have that the total sample is divided in 2 different groups from where you want to select certain number of objects randomly), so we can use the formula of hypergeometric probability for 2 groups:

`P(x=a) = \frac{{{n_(1)\choose{a}}{n_(2)\choose{n-a}}}}{{n\choose{a}}}`

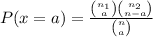
Where n₁ is the number of objects in group 1, n₂ the same but for group 2, n is the total of objects in two groups and a is the number of people we want in group 1 (depending what you consider success).

Now we are able to find the probability that we were asked for:

`P(`

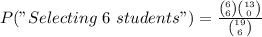
Notice I set a (being 6) under n₁ (group of students). That equation give us:

P("Jury of 6 students") = 0.000036

B. We use the same idea but we want to select people just from the faculty members:

`P(`

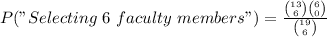
Notice i set a (being 6) under n₂ (group of the faculty), and I just changed the order. We get

P("Jury of 6 members of the faculty")=0.06324

C. Now we select people from the 2 groups, but its the same idea.

`P(`

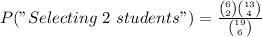
Notice "Selecting 2 students" automatically makes that you choose 4 faculty members, so you could´ve set it as "Selecting 4 faculty members" and it would be the same. When we solve, it results in

P("Jury of 2 students and 4 members of the faculty")=0.39528