Question

At 17 Celsius a sample of gas Has a volume of 580ml. If the volume is increased to 700ml, What will the temperature be in Celsius

Answer 1

77 °C

Step-by-step explanation:

This looks like a case where we can use Charles’ Law:

`(V_(1))/(T_(1)) =(V_(2))/(T_(2))`

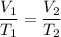
Data:

V₁ = 580 mL; T₁ = 17 °C

V₂ = 700 mL; T₂ = ?

Calculations:

(a) Convert the temperature to kelvins

T₁ = (17 + 273.15) K = 290.15 K

(b) Calculate the temperature

`\begin{array}{rcl}\frac{\text{580 mL}}{\text{290.15 K}} &=&\frac{\text{700 mL}}{T_(2)}\\\\\frac{\text{1.990}}{\text{1 K}} & = & (700)/(T_(2))\\\\1.990T_(2) & = & \text{700 K}\\T_(2) & = & \textbf{350 K}\\\end{array}`

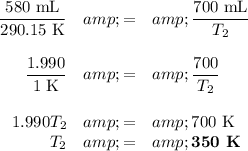
(c) Convert the temperature back to Celsius

T₂ = (350 – 273.15) °C = 77 °C