Answer:
The required probability is 0.94
Explanation:
Consider the provided information.
There are 400 refrigerators, of which 40 have defective compressors.
Therefore N = 400 and X = 40
The probability of defective compressors is:
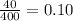
It is given that If X is the number among 15 randomly selected refrigerators that have defective compressors,
That means n=15
Apply the probability density function.

We need to find P(X ≤ 3)
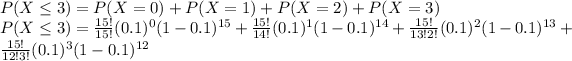
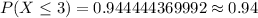
Hence, the required probability is 0.94