Question

Consider a large shipment of 400 refrigerators, of which 40 have defective compressors. If X is the number among 15 randomly selected refrigerators that have defective compressors, describe a less tedious way to calculate (at least approximately) P(X ≤ 3) than to use the hypergeometric pmf. We can approximate the hypergeometric distribution with the distribution if the population size and the number of successes are large. Here n = and p = M/N = . Approximate P(X ≤ 3) using that method. (Round your answer to three decimal places.) P(X ≤ 3) ≈

Answer 1

The required probability is 0.94

Explanation:

Consider the provided information.

There are 400 refrigerators, of which 40 have defective compressors.

Therefore N = 400 and X = 40

The probability of defective compressors is:

`(40)/(400)=0.10`

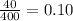
It is given that If X is the number among 15 randomly selected refrigerators that have defective compressors,

That means n=15

Apply the probability density function.

`P(X=x)=^nC_xp^x(1-p)^(n-x)`

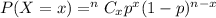
We need to find P(X ≤ 3)

`P(X\leq3) =P(X=0)+P(X=1)+P(X=2)+P(X=3)\\P(X\leq3) =(15!)/(15!)(0.1)^0(1-0.1)^(15)+(15!)/(14!)(0.1)^1(1-0.1)^(14)+(15!)/(13!2!)(0.1)^2(1-0.1)^(13)+(15!)/(12!3!)(0.1)^3(1-0.1)^(12)\\`

`P(X\leq3) =0.944444369992\approx 0.94`

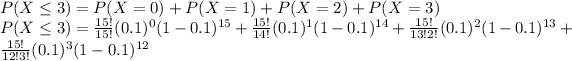
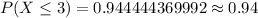
Hence, the required probability is 0.94