Question

Gold forms a substitutional solid solution with silver. Calculate the number of gold atoms per cubic centimeter (in atoms/cm3) for a silver-gold alloy that contains 17 wt% Au and 83 wt% Ag. The densities of pure gold and silver are 19.32 and 10.49 g/cm3, respectively, and their respective atomic weights are 196.97 and 107.87 g/mol. atoms/cm3

Answer 1

Na = 5.911 ×
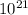`10^(21)` atoms/cm³

Step-by-step explanation:

given data

silver-gold alloy C Au = 17 wt%

densities ρ Au = 19.32 g/cm³

densities ρ Ag = 10.49 g/cm³

atomic weights A Au = 196.97 g/mol

atomic weights A Ag = 107.87 g/mol

solution

we will apply here formula for number of gold atoms that is

Na =
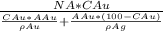`(NA * C Au)/((C Au * A Au)/(\rho Au) + (A Au * (100-C Au))/(\rho Ag))` ............................1

here NA is Avogadro's number and ρ is density of two element and A is atomic weight

put here value

Na =
`(6.022*10^(23) * 0.17)/((0.17 * 196.97)/(19.32) + (196.97 * (100-0.17))/(10.49))`

Na = 5.911 ×
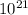`10^(21)` atoms/cm³