Question

The coordinates of the vertices of A DEF are D(-4,1), E(3. – 1), and F(-1, – 4)

Which statement correctly describes whether A DEF is a right triangle?
O
A DEF is not a right triangle because no two sides are perpendicular.
A DEF is a right triangle because DE is perpendicular to EF
A DEF is a right triangle because DF is perpendicular to EF
A DEF is a right triangle because DE is perpendicular to DF

Answer 1

ΔDEF is not a right triangle because no two sides are perpendicular.

Explanation:

The coordinates of the vertices of ΔDEF are given to be D(-4,1), E(3,-1) and F(-1,-4).

Now length of DE is given by
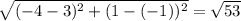`\sqrt{(-4-3)^(2)+(1-(-1))^(2)  } =√(53)` units

length of EF is given by
`\sqrt{(3-(-1))^(2)+(-1-(-4))^(2)  }=√(25)` units

and length of FD is given by
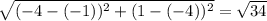`\sqrt{(-4-(-1))^(2)+(1-(-4))^(2)  } =√(34)` units.

Therefore, 53 ≠ 25+34

Hence, the length of the sides does not support the Pythagoras theorem.

So, ΔDEF is not a right triangle because no two sides are perpendicular. (Answer)