Question

Identify the initial value in each formula below, and state whether the formula models exponential growth or

exponential decay. Justify your responses.
b. f(t) = 2 (5 /3) ^t

Answer 1

Intial Value: f(t) = 2 , Exponential Growth

Explanation:

To find the initial value, all we have to do is find the value of f(t) at t = 0

In this case the given equation becomes

`f(t) = 2((5)/(3))^0`

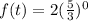
from the law of indices we know that any number with the power 0 is equal to 1 (except 0 with the power 0)

`a^0 = 1`

hence the above equation becomes

`f(t) = 2(1)\\ f(t) = 2`

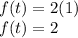
so the initial value is 2.

To find out whether this is exponential growth or exponential decay we need to see whether the base value of the power t is less than 1 or greater than 1, i.e. from

`((5)/(3) )^t`

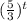
is

`(5)/(3)` > 1 or
`(5)/(3)` < 1

if the value is greater, then with each increment in power, the total value will increase while if it is less than 1 then with each increment in power the total value will decrease.

Hence since
`(5)/(3)` > 1 then this is an exponential growth