Question

If a person takes a given dosage dd of a particular medication, then the formula ff(tt) = dd (0.8)tt represents the

concentration of the medication in the bloodstream tt hours later. If Charlotte takes 200 mg of the medication at
6: 00 a.m., how much remains in her bloodstream at 10: 00 a.m.? How long does it take for the concentration to
drop below 1 mg?

Answer 1

It remais 128 mg of the medication at 10:00 a.m.

It takes 1 day for the concentration to drop below 1 mg

Explanation:

The formula of the decays of the concentration of the medications is:

`f(t) = d*(0.8)^t`

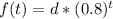
So, if she takes the medication ate 6:00 a.m., at 10:00 a.m., t= 2, so:

f(2) = 200*(0.8)²

f(2) = 128 mg

For the concentration drop below 1 mg:

`1 = 200*(0.8)^t`

`(0.8)^t = 0.005`

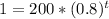
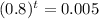
Applying ln:

`ln(0.8)^t = ln0.005`

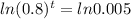
t*ln0.8 = -5.2983

-0.2231t = -5.2983

t = 23.74 hours

So, it will take 24 hours, or 1 day, for the concentration drop below 1 mg.