Answer:
1) 1.808 *10^8 vacancies per cm^3
2) 101,64ºC
Step-by-step explanation:
You can use the following equation relating the number of vacancies with the energy required to produce them and the temperature:
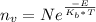
Where N is the number atoms per unit of volume, you can calculate this number with the density of copper:
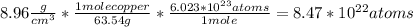
And you can substitute all values in the equation:
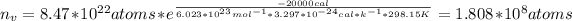
Now you solve for temperature and and use n as 1000 times the value of before:
