Question

Identify the initial value in each formula below, and state whether the formula models exponential growth or

exponential decay. Justify your responses.
d. f(t) = 2 / 3 (1 / 3)^t

Answer 1

Initial Value is
`f(t) = (2)/(3)`, This function follows exponential decay

Explanation:

The initial value of any time based function is the value of f(t) at t = 0. For calculating the initial value of this function all we have to do is insert 0 as the value of t.

`f(0) = (2)/(3) (1)\\ f(0) = (2)/(3)`

Hence the initial value is
`(2)/(3)`

To find out whether this function is exponential growth or decay we need to ascertain whether the base value of the power t is greater than or lesser than 1

In this case the base value of
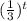`((1)/(3) )^t` is
`(1)/(3)` which is lesser than 1, hence this function is exponential decay since with each increase in power the total value will decrease,i.e.

`=((1)/(3) )^0 = 1\\\ = ((1)/(3))^1 = 0.333\\\ =((1)/(3))^2 = 0.1111\\  =((1)/(3))^3 = 0.037\\ .\\ .\\ .\\`

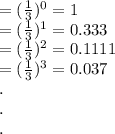
This can also be proven from the graph below