Answer:
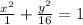
Explanation:
The center of the ellipse at the origin, and (1,0) and (0,4) are the vertex and co-vertex of it.
Therefore, the major and minor axis of the ellipse is X-axis and Y-axis respectively.
And the standard form of the equation of ellipse is
 , where a = half of major axis length and b = half of minor axis length.
, where a = half of major axis length and b = half of minor axis length.
So, a = 1 and b = 4.
Therefore, the equation of the given ellipse is
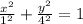
⇒
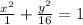 (Answer)
(Answer)