Answer:
At least 15 households have between 0 and 4 televisions.
Explanation:
Chebychev's Theorem:
P(|X-μ|>kσ)≤
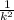
μ= mean
σ= standard deviation
k= number of typical deviations
It is also expressed as:
P(μ-kσ<X<μ+kσ)≥
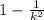
Using Chebychev's Theorem, we determine:
P(0<X<4)
μ-kσ=0 ⇒ 2-k·1=0 ⇒k=2
μ+kσ=4 ⇒ 2+k·1=4 ⇒k=2
P(0<X<4)=
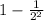 =0.75
=0.75
For a sample n=20,
0.75×20=15
At least 15 households have between 0 and 4 televisions.