Question

From a sample with n=20​, the mean number of televisions per household is 2 with a standard deviation of 1 television. Using​ Chebychev's Theorem, determine at least how many of the households have between 0 and 4 televisions. At least nothing of the households have between 0 and 4 televisions.

Answer 1

At least 15 households have between 0 and 4 televisions.

Explanation:

Chebychev's Theorem:

P(|X-μ|>kσ)≤
`(1)/(k^2)`

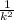
μ= mean

σ= standard deviation

k= number of typical deviations

It is also expressed as:

P(μ-kσ<X<μ+kσ)≥
`1-(1)/(k^2)`

Using​ Chebychev's Theorem, we determine:

P(0<X<4)

μ-kσ=0 ⇒ 2-k·1=0 ⇒k=2

μ+kσ=4 ⇒ 2+k·1=4 ⇒k=2

P(0<X<4)=
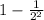`1-(1)/(2^2)`=0.75

For a sample n=20,

0.75×20=15

At least 15 households have between 0 and 4 televisions.