Answer: The 10th term is 19
Explanation:
For a sequence to be an arithmetic sequence, then there exist a common difference.
 How do we calculate common difference?
How do we calculate common difference?
 Common difference is calculated by subtracting the first term from the second term, subtracting the second term from the third term and so on.
Common difference is calculated by subtracting the first term from the second term, subtracting the second term from the third term and so on.
 From the sequence given , 3 + x, 9 + 3x, 13 + 4x, .. , calculating common difference implies
From the sequence given , 3 + x, 9 + 3x, 13 + 4x, .. , calculating common difference implies
 (9+3x) – ( 3 +x) = 13 + 4x – ( 9 + 3x)
(9+3x) – ( 3 +x) = 13 + 4x – ( 9 + 3x)
 Expanding, we have
Expanding, we have
 9 + 3x – 3 – x = 13 + 4x – 9 – 3x
9 + 3x – 3 – x = 13 + 4x – 9 – 3x
 ⇒9 – 3+3x –x = 13 – 9 +4x – 3x
⇒9 – 3+3x –x = 13 – 9 +4x – 3x
 ⇒6 + 2x = 4 + x
⇒6 + 2x = 4 + x
 Collecting the like terms , we have
Collecting the like terms , we have
 2x – x = 4 – 6
2x – x = 4 – 6
 which gives X = -2
which gives X = -2
 Since the value of x is gotten now , we can get what the given sequence looks like by substituting the value of x into each term given, the sequence becomes:
Since the value of x is gotten now , we can get what the given sequence looks like by substituting the value of x into each term given, the sequence becomes:
 3 + (-2), 9 + 3(-2), 13 + 4(-2) +...
3 + (-2), 9 + 3(-2), 13 + 4(-2) +...
 Which gives
Which gives
 1 , 3 ,5, …
1 , 3 ,5, …
 We can therefore note that the common difference is 2
We can therefore note that the common difference is 2
 check: 3 - 1 = 5 -3 = 2
check: 3 - 1 = 5 -3 = 2
 (b) To calculate the tenth term , we use the general formula for calculating nth term , which is given as
(b) To calculate the tenth term , we use the general formula for calculating nth term , which is given as

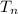 = a + (n-1)d
= a + (n-1)d
 Where n is the number of terms , a is the first term and d is the common difference,
Where n is the number of terms , a is the first term and d is the common difference,
 Therefore,
Therefore,
 = 1 + ( 10-1)x2
= 1 + ( 10-1)x2
 = 1 + 18
= 1 + 18
 = 19
= 19
Therefore the 10th term is 19