Question

3 + x, 9 + 3x, 13 + 4x, ... is an arithmetic sequence for some real number x.

b. Find the 10th term of the sequence.

Answer 1

Answer: The 10th term is 19

Explanation:

For a sequence to be an arithmetic sequence, then there exist a common difference.

`\\`How do we calculate common difference?

`\\`Common difference is calculated by subtracting the first term from the second term, subtracting the second term from the third term and so on.

`\\`From the sequence given , 3 + x, 9 + 3x, 13 + 4x, .. , calculating common difference implies

`\\`(9+3x) – ( 3 +x) = 13 + 4x – ( 9 + 3x)

`\\`Expanding, we have

`\\`9 + 3x – 3 – x = 13 + 4x – 9 – 3x

`\\`⇒9 – 3+3x –x = 13 – 9 +4x – 3x

`\\`⇒6 + 2x = 4 + x

`\\`Collecting the like terms , we have

`\\`2x – x = 4 – 6

`\\` which gives X = -2

`\\`Since the value of x is gotten now , we can get what the given sequence looks like by substituting the value of x into each term given, the sequence becomes:

`\\`3 + (-2), 9 + 3(-2), 13 + 4(-2) +...

`\\`Which gives

`\\`1 , 3 ,5, …

`\\`We can therefore note that the common difference is 2

`\\`check: 3 - 1 = 5 -3 = 2

`\\`(b) To calculate the tenth term , we use the general formula for calculating nth term , which is given as

`\\`
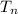`T_(n)` = a + (n-1)d

`\\`Where n is the number of terms , a is the first term and d is the common difference,

`\\`Therefore,
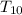`T_(10)` = 1 + ( 10-1)x2

`\\`= 1 + 18

`\\` = 19

Therefore the 10th term is 19