Answer and explanation:
Given : Examination of court records in a particular state shows that the mean sentence length for first-offense drug dealers is 26 months with a standard deviation of 2 months. The records show that the sentence lengths are normally distributed.
i.e. Mean
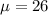 , Standard deviation
, Standard deviation
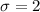
Using Z-score formula,
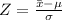
1) What is the Z score for a 23 month sentence length? What is the probability of getting a sentence below that?
The Z score value for a
 is given by,
is given by,
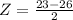
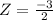
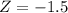
The probability of getting a sentence below that is
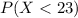
i.e.
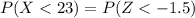
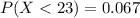
2) A defense attorney is concerned that his client's sentence was unusually harsh at 30 months. What percent of sentences are 30 months or longer? Calculate the Z score and report the area.
The Z score value for a
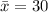 is given by,
is given by,
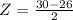
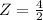

The probability of getting a sentence below that is
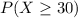
i.e.
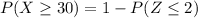
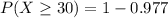
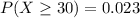
Into percentage,

3) Would you consider a 30 month sentence harsh? Explain
Since the percentage for 30 months or greater is harsh because the smaller value of percentage of
