Answer: The largest dimensions that are possible would be 50 foot by 125 foot.
Explanation:
Since we have given that
Amount a farmer has available = $1500
Let x be the side perpendicular to the river.
Let y be the side parallel to the river.
Number of section perpendicular to the river = 3
cost of material for the side parallel to the river = $6 per foot
Cost of material for the side perpendicular to the river = $5 per foot
So, total cost becomes
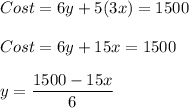
Area would be
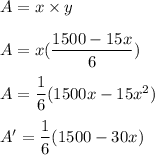
Now, put A' = 0 to get the critical points.
So, it becomes,
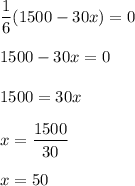
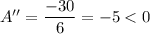
so, at x= 50 it will give maximum dimensions.
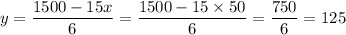
So, the largest dimensions that are possible would be 50 foot by 125 foot.