Question

A man walks for x hours at a speed of

(x + 1) km/h and cycles for (x - 1) hours at
a speed of (2x + 5) km/h. If the total distance
travelled is 90 km, x

Answer 1

Given:

A man walks for x hours at a speed of (x + 1) km/h and cycles for (x - 1) hours at a speed of (2x + 5) km/h.

Total distance travelled is 90 km.

To find:

The value of x.

Solution:

We know that,

`Speed=(Distance)/(Time)`

`Speed* Time=Distance`

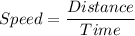
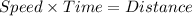
A man walks for x hours at a speed of (x + 1) km/h, so walking distance is

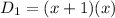`D_1=(x+1)(x)` km

The man cycles for (x - 1) hours at a speed of (2x + 5) km/h, so the cycling distance is

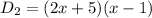`D_2=(2x+5)(x-1)` km

Now,

Total distance = 90 km

`D_1+D_2=90`

`(x+1)x+(2x+5)(x-1)=90`

`x^2+x+2x^2-2x+5x-5-90=0`

`3x^2+4x-95=0`

`3x^2+19x-15x-95=0`

`x(3x+19)-5(3x+19)=0`

`(3x+19)(x-5)=0`

`3x+19=0\text{ and }x-5=0`

`x=(-19)/(3)\text{ and }x=5`

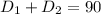
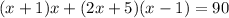
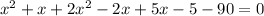
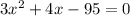
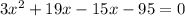
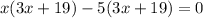
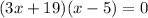
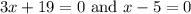
Time cannot be negative. So, the only possible value of x is 5.