Answer:
(C) 0.368
Explanation:
The Poisson distribution models the probability that an event occurs k times in a given fix interval of time.
Is defined by the probability function
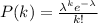
where
k = number of events in the given interval
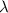 = average number of events in the given interval.
= average number of events in the given interval.
In our specific case, the given interval of time is 12 seconds, and
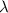 = 1 (1 car every 12 seconds).
= 1 (1 car every 12 seconds).
As the old wombat requires 12 seconds to cross the highway, it might survive if only 1 car arrives over those 12 seconds.
The probability of this fact is P(1)
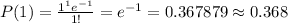
So, the right answer is (C), 0.368