Question

Find 3 consecutive even integers such that the sum of twice the smallest and three times the largest is 42

Answer 1

6, 8, 10

Explanation:

Consecutive even integers are in the form:

2, 4, 6 ... etc

As we can see, they have a "gap" of 2 in between. Thus, if we let the first number be "x", the next consecutive even number would be "x + 2" and the next one would be "x + 4".... and so on...

We have our numbers: x, x + 2, x + 4

It says the sum of twice the smallest and 3 times the largest is 42. We can write:

`2x + 3(x+4) = 42`

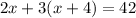
This is the equation. Now we solve for x and find all the 3 consecutive even integers. Shown below:

`2x + 3(x+4) = 42\\2x + 3x + 12 = 42\\5x = 42 - 12\\5x = 30\\x = (30)/(5)\\x=6`

The 3 integers are 6, 8, and 10