Answer:
a) 0.0167
b) 0
c) 5.948
Explanation:
We are given the following information in the question:
Mean, μ = 6.16 ounces
Standard Deviation, σ = 0.08 ounces
We are given that the distribution of fill volumes of bags is a bell shaped distribution that is a normal distribution.
Formula:
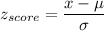
a) Standard deviation of 23 bags
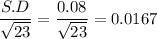
b) P( fill volume of 23 bags is below 5.95 ounces)
P(x < 5.95)
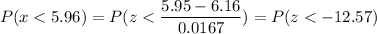

Calculation the value from standard normal z table, we have,
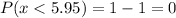
c) P( fill volume of 23 bags is below 6 ounces) = 0.001
P(x < 6) = 0.001

Calculation the value from standard normal z table, we have,


If the mean will be 5.948 then the probability that the average of 23 bags is below 6.1 ounces is 0.001.