Question

A scientist needs 120 milliliters of a 20% acid solution for an experiment. The lab has available a 25% and a 10% solution. How many liters of the 25% and how many liters of the 10% solutions should the scientist mix to make the 20% solution?

Answer 1

the required quantity of solution of 10% is 40 ml

the required quantity of solution of 25% = 80 ml

Step-by-step explanation:

let the required quantity of solution of 10% be x

and quantity of solution of 25% be (120 - x) ml

Hence, quantity of acid in x ml of 10 percentage solution is
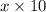`x* 10%`and similarly for 25% solution be
`( 120-x) * 25\%`

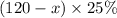
therefore total amount of acid is
`x* 10\% +  ( 120-x) * 25\%`

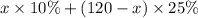
we need total solution of 120 ml of 20% so we have

`x* 10\% +  ( 120-x) * 25\% = 120 * 20\%`

after solving we get

`(x)/(10) -(x)/(4) = 24 - (120)/(4)`

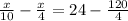
solving for x we get

x = 40

therefore ,

the required quantity of solution of 10% is 40 ml

the required quantity of solution of 25% = 80 ml