Answer:

Explanation:
Let
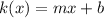 be the expression for the linear function k(x), where m is the slope of the function and this function passes through the point (1,8).
be the expression for the linear function k(x), where m is the slope of the function and this function passes through the point (1,8).
Thus,
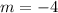 and the function expression is
and the function expression is

If the graph of the function passes through the point (1,8), then its coordinates satisfy the function expression. Substitute them:
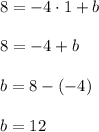
Hence,
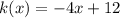
The graph of this function intersects the x-axis at k(x)=0, then

Zero of the function is x=3