Question

the graph of linear function k has slope -4 and passes through (1,8). what is the zero in function k? ​

Answer 1

`x=3`

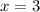
Explanation:

Let
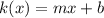`k(x)=mx+b` be the expression for the linear function k(x), where m is the slope of the function and this function passes through the point (1,8).

Thus,
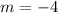`m=-4` and the function expression is

`k(x)=-4x+b`

If the graph of the function passes through the point (1,8), then its coordinates satisfy the function expression. Substitute them:

`8=-4\cdot 1+b\\ \\8=-4+b\\ \\b=8-(-4)\\ \\b=12`

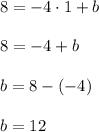
Hence,

`k(x)=-4x+12`

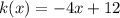
The graph of this function intersects the x-axis at k(x)=0, then

`-4x+12=0\\ \\-4x=-12\\ \\x=3`

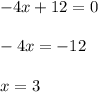
Zero of the function is x=3