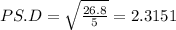Question

Consider the data set. 2, 5, 6, 7, 9 (a) Find the range. 7 Correct: Your answer is correct. (b) Use the defining formula to compute the sample standard deviation s. (Round your answer to two decimal places.) 2.7 Incorrect: Your answer is incorrect. (c) Use the defining formula to compute the population standard deviation σ. (Round your answer to two decimal places.) -6.23 Incorrect: Your answer is incorrect.

Answer 1

The range of the data set is 7. The sample standard deviation (s) is 2.54.

Step-by-step explanation:

The range of a data set is the difference between the maximum and minimum values. In this case, the maximum value is 9 and the minimum value is 2, so the range is 9 - 2 = 7.

To compute the sample standard deviation, we use the formula √((sum((x - mean)²))/(n - 1)), where x is each data point, mean is the average of the data points, and n is the number of data points.

1. Calculate the mean: (2 + 5 + 6 + 7 + 9)/5 = 29/5 = 5.8
2. Calculate the squared differences from the mean for each data point: (2 - 5.8)² = 13.44, (5 - 5.8)² = 0.64, (6 - 5.8)²= 0.04, (7 - 5.8)^2 = 1.44, (9 - 5.8)² = 10.24
3. Sum the squared differences: 13.44 + 0.64 + 0.04 + 1.44 + 10.24 = 25.8
4. Divide the sum by (n - 1): 25.8/(5 - 1) = 25.8/4 = 6.45
5. Take the square root: √(6.45) = 2.54

So the sample standard deviation (s) is 2.54, rounded to two decimal places.

Answer 2

A) 7

B) 2.588

C) 2.3151

Step-by-step explanation:

We are given the following data set:

2, 5, 6, 7, 9

Formula:

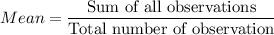
`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

Mean =
`\displaystyle(29)/(5) = 5.8`

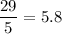
a) Range

= Highest value - Lowest Value = 9 - 2 = 7

b) Sample standard deviation

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

Sum of squares = 14.44 + 0.64 + 0.04 + 1.44 + 10.24 = 26.8

`SS.D = \sqrt{(26.8)/(4)} = 2.588`

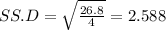
c) Population standard deviation

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n}}`

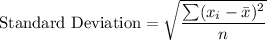
where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

Sum of squares = 14.44 + 0.64 + 0.04 + 1.44 + 10.24 = 26.8

`PS.D = \sqrt{(26.8)/(5)} = 2.3151`