2 Answers

Bran Van Der Meer · Answer 1 · 2020-04-13T04:13:08+0000

Answer : The value of x and y are, 64° and 50° respectively.

Step-by-step explanation :

As we know that, ABCD is a trapezium and AB || CD. So, the sum of opposite angles are 180°

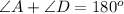
$\angle A+\angle D=180^o$

Given:

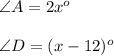
$\angle A=2x^o\\\\\angle D=(x-12)^o$

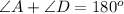
$\angle A+\angle D=180^o$

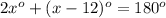
2x^o+(x-12)^o=180^o

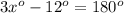
3x^o-12^o=180^o

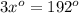
3x^o=192^o

x=64^o

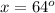
and,

Given:

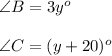
$\angle B=3y^o\\\\\angle C=(y+20)^o$

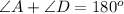
$\angle A+\angle D=180^o$

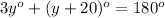
3y^o+(y+20)^o=180^o

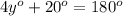
4y^o+20^o=180^o

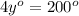
4y^o=200^o

y=50^o

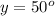
Thus, the value of x and y are, 64° and 50° respectively.

Please log in or register to add a comment.