Question

A proton circulates in a cyclotron, beginning approximately at rest at the center. Whenever it passes through the gap between dees, the electric potential difference between the dees is 120 V. (a) By how much does its kinetic energy increase with each passage through the gap? (b) What is its kinetic energy as it completes 107 passes through the gap? (c) Let r107 be the radius of the proton's circular path as it completes those 107 passes and enters a dee, and let r108be its next radius, as it enters a dee the next time. By what percentage does the radius increase when it changes from r107 to r108? That is, what is percentage increase = (r108 - r107)/r107*100%?

Answer 1

(a) 120 eV

(b) 12.840 keV

(c) 0.466%

Solution:

As per the question:

The potential difference between the dees, V = 120 V

No. of passes, n = 107

Now,

(a) The potential energy can be given as 'qV' but by the principle of conservation of energy, this energy with each pass is converted into the kinetic energy of the particle which is given as 120 eV

Thus

The increase in Kinetic energy,
`\Delta KE = 120\ eV`

(b) Kinetic energy on completion of 107 passes is given by:

`KE = n\Delta KE = 107* 120\ eV = 12.840\ keV`

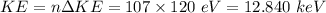
(c) The velocity of the particle can be calculated from its kinetic energy:

`KE = (1)/(2)m_(p)v^(2) = 12.840\ keV = 120n\ eV`

Thus

`v = \sqrt{(240ne)/(m_(p))}`

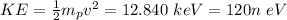
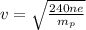
Thus radius can be given as:

`R = (m_(p))/(Bq)(\sqrt{(240ne)/(m_(p))})`

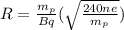
where

B = Magnetic field

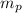`m_(p)` = mass of proton

Therefore, we can write that:

`R = √(n)`

Thus the percentage increase in radius from n = 107 to n = 108 is given by:

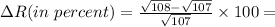`\Delta R(in\ percent) = (√(108) - √(107))/(√(107))* 100 =` = 0.466 %