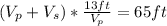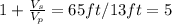Answer:
person walk rate:
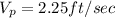
Step-by-step explanation:
A person walking on the moving sidewalk moves at a velocity:
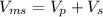
Where
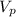 is the velocity of the person and
is the velocity of the person and
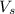 the velocity of the sidewalk.
the velocity of the sidewalk.
The distance traveled in a time t is t times the velocity:

I this same time a person on a nonmoving sidewalk travels 13ft:

Solving this for t:
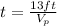
Replacing this on the equation for the moving sidewalk: