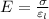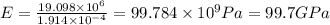Question

Consider a cylindrical specimen of some hypothetical metal alloy that has a diameter of 10.0 mm. A tensile force of 1500 N produces an elastic reduction in diameter of 6.7 × 10–4 mm. Compute the elastic modulus of this alloy, given that Poisson’s ratio is 0.35. Express the answer in GPa to three significant figures. Answer:

Answer 1

The elastic modulus is 99.7 GPa

Solution:

As per the question:

Diameter of the metal alloy, D = 10.0 mm = 0.01 m

Tensile force, F = 1500 N

Elastic reduction in the diameter of the metal alloy,
`\Delat D = 6.7* 10^(- 4) mm = 6.7* 10^(- 7) m`

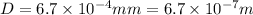
Poisson's ratio,
`\mu = 0.35`

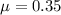
Now,

Lateral strain is given by:

`\varepsilon_(D) = (\Delta D)/(D) = (6.7* 10^(- 4))/(10) = 6.7* 10^(- 5)`

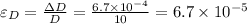
Longitudinal strain,
`\varepsilon_(l)`:

`\varepsilon_(l) = (\varepsilon_(D))/(\mu) = (6.7* 10^(- 5))/(0.35) = 1.914* 10^(- 4)`

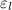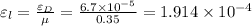
Now, stress is given by:

`\sigma = (F)/(Area,\ A)`

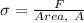
where

`A = \pi ((d)/(2))^(2) = \pi ((0.01)/(2))^(2) = 7.854* 10^(- 5) m^(2)`

Now,

`\sigma = (1500)/(7.854* 10^(- 5)) = 19.098* 10^(6) = 19.098 MPa`

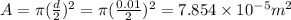
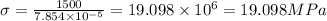
Now, the elastic modulus is given by:

`E = (\sigma)/(\varepsilon_(l))`

`E = (19.098* 10^(6))/(1.914* 10^(- 4)) = 99.784* 10^(9)Pa = 99.7 GPa`