Question

Suppose the probability density function of the length of computer cables is f left-parenthesis x right-parenthesis equals 0.1 from 1200 to 1210 millimeters. a) Determine the mean and standard deviation of the cable length. Mean = Entry field with correct answer 1205 millimeters Standard deviation = Entry field with correct answer 2.89 millimeters (Round the answer to 2 decimal places.) b) If the length specifications are 1192less-than x less-than 1204, what proportion of cables is within specifications?

Answer 1

a) Mean = 1205

Standard Deviation = 2.89

b) P( 1192 < x < 1204) = 0.4

Explanation:

We are given the following information in the question:

`f(x) = 0.1\\`

a = 1200, b = 1210

We are given a uniform distribution.

a) Mean:

`\mu = \displaystyle(a+b)/(2)\\\\\mu = (1200+1210)/(2) = 1205`

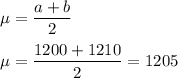
Standard Deviation:

`\sigma = \sqrt{\displaystyle((b-a)^2)/(12)}\\\\= \sqrt{\displaystyle((1210-1200)^2)/(12)} = √(8.33) = 2.89`

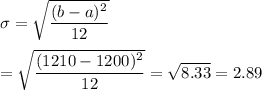
b) P( 1192 < x < 1204)

`=\displaystyle\int_(1192)^(1204) f(x) dx\\\\=\displaystyle\int_(1200)^(1204) (0.1) dx\\\\=0.1[x]_(1200)^(1204) = (0.1)(1204-1200) = 0.4`