Answer:
The probability that one of the factory's bikes passed inspection and came off assembly line B is 0.564.
Explanation:
Given : A bicycle factory runs two assembly lines, A and B. 97% of line A's products pass inspection and 94% of line B's products pass inspection. 40% of the factory's bikes come off assembly line B and the rest come off line A.
To find : The probability that one of the factory's bikes passed inspection and came off assembly line B ?
Solution :
The probability of line B's is P(B)= 40%=0.4
The probability of line A's is P(A)=100-40= 60%=0.6
Let E be the passes inspection.
The probability of line A's products pass inspection is P(E/A)=97%=0.97
The probability of line B's products pass inspection is P(E/B)=94%=0.94
The probability that one of the factory's bikes passed inspection and came off assembly line B is
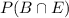
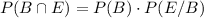
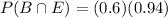
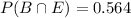
Therefore, The probability that one of the factory's bikes passed inspection and came off assembly line B is 0.564.