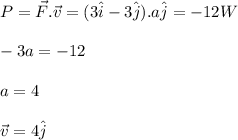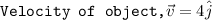Answer:
a) Instantaneous rate at which the force does work on the object = -6 W
b)
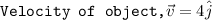
Step-by-step explanation:
a) Given that
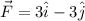
and
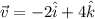
Instantaneous rate at which the force does work on the object is called power.
Power is the dot product of force and velocity.
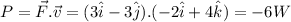
Instantaneous rate at which the force does work on the object = -6 W
b) Here given that
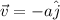
Power = -12 W