Answer:
0xFEE₁₆ = 7756₈
Explanation:
Convert the hexadecimal number to decimal first
0xFEE
E = 14
F = 15
Then convert them to binary
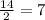
Remainder = 0
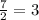
Remainder = 1
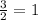
Quotient = 1
Remainder = 1
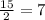
Remainder = 1
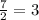
Remainder = 1
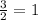
Quotient = 1
Remainder = 1
0 F E E
0000 1111 1110 1110
Take groups of three
and multiply with
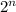 where n is the place of the digit
where n is the place of the digit
111 111 101 110
4,2,1 4,2,1 4,2,1 4,2,1
4+2+1 4+2+1 4+0+1 4+2+0
7756
So, 0xFEE₁₆ = 7756₈