Question

A furnace wall consisting of 0.25 m of fire clay brick, 0.20 m of kaolin, and a 0.10‐m outer layer of masonry brick is exposed to furnace gas at 1370 K with air at 300 K adjacent to the outside wall. The inside and outside convective heat‐transfer coefficients are 115 and 23 W/m2 ⋅ K, respectively. Determine the heat loss per square foot of wall and the temperature of the outside wall surface under these conditions.

Answer 1

q=1910.71 W/m²

T=383.07 K

Step-by-step explanation:

Given that

L₁=0.25 m ,K₁=1.13 W/(m.K)

L₂=0.2 m , K₂=1.45 W/(m.K)

L₃= 0.1 m , K₃=0.66 W/(m.K)

h₁=115 W/(m².K)

h₂=23 W/(m².K)

The total thermal resistance

`R=(L_1)/(K_1A)+(L_2)/(K_2A)+(L_3)/(K_3A)+(1)/(h_1A)+(1)/(h_2A)\ K/W`

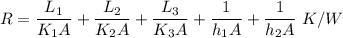
Now by putting the values

Put A= 1 m² ( To find heat transfer per unit area)

`R=(L_1)/(K_1A)+(L_2)/(K_2A)+(L_3)/(K_3A)+(1)/(h_1A)+(1)/(h_2A)\ K/W`

`R=(0.25)/(1.13)+(0.2)/(1.45)+(0.1)/(0.66)+(1)/(115)+(1)/(23)\ K/W`

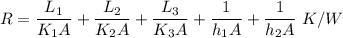
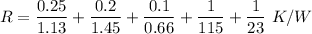
R= 0.56 K/W

We know that

q= ΔT/R

Here ΔT = 1370 - 300 K =1070 K

Now by putting the values

q= 1070/0.56

q=1910.71 W/m²

Lets T is the outside surface temperature

q = h₂ ( T- 300)

Now by putting the values

1910.71 = 23 ( T- 300)

T=383.07 K